Understanding and Sound of Pascal’s law is equipped with Principles, Formulas (equations), Sample Questions and Application of Pascal’s law
Continuing the previous article on Ohm’s law and also Kirchhoff’s law, this time we will review in detail the law in another electrical science, namely Pascal’s law.
Paskal law is one of the laws in the field of physics that is often used in everyday life, including in static fluids, For a more complete explanation of the meaning, sound and formula, consider the following explanation.
Definition of Pascal’s Law
Via : www.tec-science.com
Pascal ‘s Law is a law that contains the principle provisions of static (immobile) fluids. When there is external pressure exerted on a closed fluid system, the pressure will be continued in various directions equally and continue to increase in proportion to the amount of pressure from outside applied.
In 1653, French philosopher and scientist Blaise Pascal released the results of his research on ‘Equilibrium of Fluids’ which contained the principle of static fluids.
A static fluid is a fluid that does not move. When the fluid is not flowing, it is in static equilibrium. Under these conditions, the total force on each part of the fluid must be zero.
In the study, Pascal concluded that the pressure changes applied to the closed fluid are passed undiminished throughout the fluid and to the walls of the liquid container.
In addition, another conclusion is also obtained that the total pressure in the fluid is the sum of pressures from different sources. It was this theory that proved Pascal’s experiments on the basis of hydraulics.
Examples of tools whose working principles are based on Pascal’s law in everyday life are Hydrometers, Ponton Bridges, and tools that utilize hydraulic systems such as hydraulic pumps, hydraulic disc brakes, and hydraulic jacks.
Pascal’s Law
“Pascal’s law states that an external static pressure exerted on a closed fluid system will be transmitted evenly in all directions.”
In closed fluid conditions, the properties of atoms in the fluid can move freely, the atoms transmit pressure to all parts of the fluid and the walls of the container, so that any changes in pressure in it are transmitted without decreasing in the slightest.
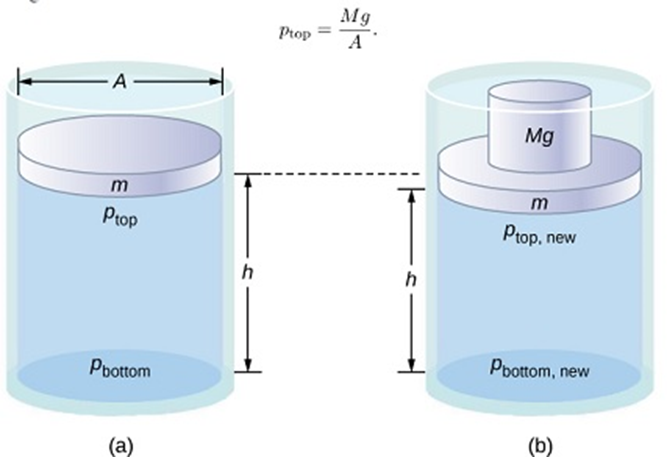
The principle of the sound of the law applies to pressure changes, for example we place water into a cylindrical container with a height (H) and cross-sectional area (A) that has a piston moving mass. (see the picture below).
Via : opentextbc.ca
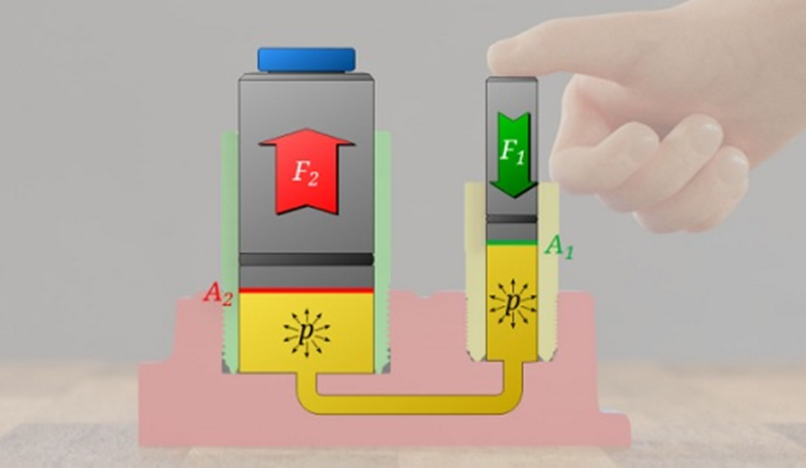
When we add weight (Mg) to the top of the piston, the pressure at the top will increase by Mg / A. This is because the additional weight load also applies above the cap area A. You can see the illustration in the example image above.
From the illustrative picture of the application of Pascal’s law above, it can be seen that the pressure in the fluid changes when the fluid is compressed. (a) The pressure in the upper layer of the fluid is different from the pressure in the lower layer. (b) Increased pressure by adding weight to the piston is equal in spread.
Pascal’s Law Formula
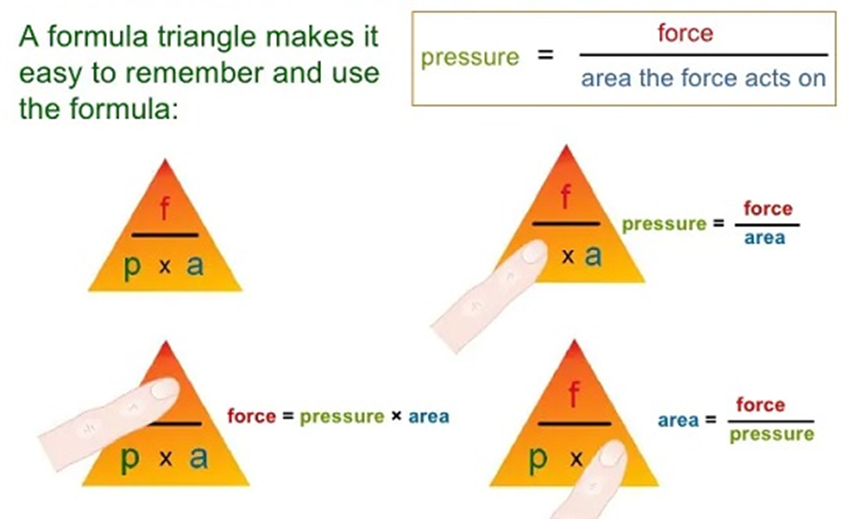
Pascal’s law formula Via : slideshare.net
Pascal’s law formulas are “[F = P.A], [P = F/A], and [A = F/P]” where F is the applied force, P is the transmitted pressure, and A is the cross-sectional area.
Learning about Pascal’s Law is incomplete if it does not discuss the formulas and equations. In Pascal’s law it is stated that the pressure of Piston 1 (the piston on the left) is equal to piston 2 (the piston on the right). It can be mathematically expressed by: P1 = P2 or Pexit = Pin
In accordance with the sound of the law where this law relates to pressure in a closed fluid system. Meanwhile, this pressure is obtained from the force divided by the cross-sectional area (P = F / A). From these equations, the equation of Pascal’s law is obtained:
P1 = P2 = 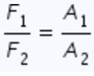
Where:
P= pressure (pascals)
F = force (N)
A = cross-sectional surface area (m2)
The formula for the distance of Pascal’s law of motion:
From the application of Pascal’s law to hydraulic mechanisms, fluids cannot escape or be added from a closed system. Therefore, the volume of liquid on the left that is pushed then pushes the piston on the right up.
The piston from the left then moves as far as h1 down while the piston on the right moves as far as h2 up. So if according to the sound of Pascal’s Law, the formula is obtained:
A1h1 = A2h2
Derivative of Pascal’s Law Formula:
Via : Byjus.com
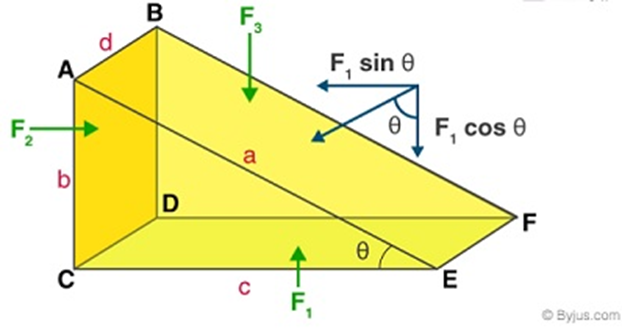
Pascal’s law states that the pressure in a fluid at rest / static is the same at all points as long as it is at the same height. This fact can be shown directly.
The image above shows an element in the interior of a fluid at rest. This AEC-BDF element is in the form of a right prism. In this principle, prismatic elements are very small.
Therefore, each part of it can be considered at the same depth from the surface of the liquid and hence, at all these points, the gravitational effect is the same. From there we get the following formula derivative equation:
Take a look at the image of the inner fluid element above!
# Suppose ad, bd, and cd are the cross-sectional areas of ABFE, ABDC, and CDFE, respectively.
# Then P1, P2, and P3 become the stress on the ABFE, ABDC, and CDFE surfaces.
# Let’s say P1 gives F1 on ABFE surface, P2 gives F2 on ABDC surface, and P3 gives F3 force on CDFE surface.
# Then the Styles in F1, F2, and F3 are:
- F1 = P1 × area of ABFE = P1 ad
- F2 = P2 × area of ABDC = P2 bd
- F3 = P3 × area of CDFE = P3 cd
![]()
# The total force on the prism will be zero because the prism is in equilibrium, so the equation is obtained:
F1 sin θ = F2F1 cos θ = F3
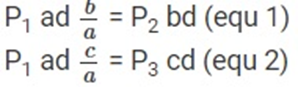
# From the two equations above, the results of the formula are obtained:
P1 = P2 and P1 = P3
∴ P1= P2= P3
Also Read: Definition of Kirchhoff’s Law
Examples of Pascal’s Law Problems
After knowing the theory, sounds and formulas of equations in Pascal’s Law, then the formula can be applied to work on problems related to Pascal’s Law. Here are some examples of Pascal’s law problems that can be a reference.
- A hydraulic pump with a cylindrical shape has a radius of 4cm and 20cm respectively. if a small suction is exerted a force pressure of 200N, how much force is the force on the large suction?
Discussion:
A1 = 4 x 10-4m2
A2 = 0.1 m2
F2 = 104 N
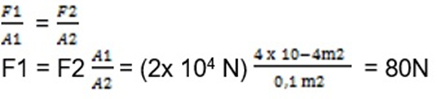
So, the force that must be exerted for such a small suction is 80N
- A hydraulic jack has suctions with an area of A1 = 15 cm² and A2 = 600 cm² respectively. If a small sucker is given a force (F1) of 500 Newtons, what is the weight of the load that can be lifted by the jack?
Discussion:
F1/F2 = A1/A2
500 N/ F2 = 15 cm²/600 cm²
F2 = ( 500 x 600) / 15
F2 = 20,000 N
- Two piston lifts on hydraulic jacks have a diameter of 60 cm and 5 cm. What is the force exerted by a larger piston when 50 N is placed on a smaller piston?
Discussion:
# Finger piston :
r = D/2
# Small piston area:
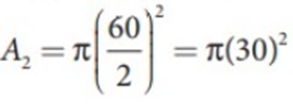
#Area large pistons:
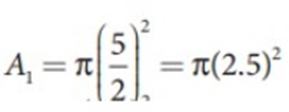
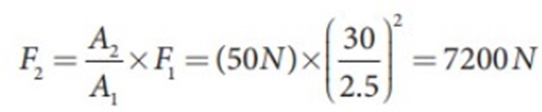
So with a force of 50 N, the jack can lift a force load of 7200 N.
- A pressure of 2000 Pa is transmitted throughout the column of fluid applied to the piston. If the piston has an area of 0.1 m2, what is the force applied?
Discussion:
F = PA
P = 2000 Pa = N/m2
A = 0.1 m2
Subtittish the value, so that F = 200 N is obtained
- PR Problem: A car will be lifted with a hydraulic jack. If a large pipe has a radius of 21cm and a small pipe has a radius of 2cm, then what force should be exerted on a small pipe if the car weighs 15,000N?
After studying some examples of Pascal’s law calculation questions above, please work on this homework question and answer in the comments column if you already know the results :)).
Application of Pascal’s Law
The discovery of Pascal’s law is not without cause, because even when it was discovered, Blaise Pascal observed from phenomena that occur in everyday life. Therefore, Pascal’s law also works and is applied in everyday life.
Examples of the application of Pascal’s law in everyday life can be seen in hydraulic jacks, hydraulic pumps, cotton press machines, and hydraulic brakes.
Pascal’s law in everyday life is applied to facilitate the work done by man. Here are some applications of daily life that utilize the working principles of Paskal Law:
-
Hydraulic Jack
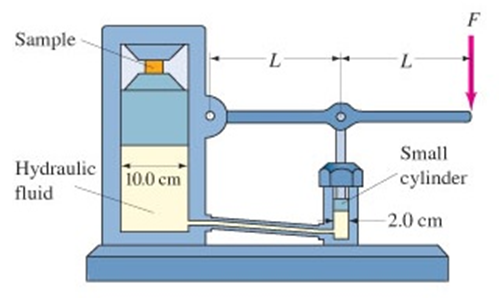
The first example of the application of Pascal’s law in everyday life is the hydraulic jack. This hydraulic jack is a tool used to lift the car when it is about to change its tires. The working principle of this tool is to use two cylinders of different sizes, namely large and small.
The way it works, when this jack is pressed, the oil in the small cylinder is depressed and flows into the large cylinder. The movement then causes a force that is able to lift weights.
-
Hydraulic Pump
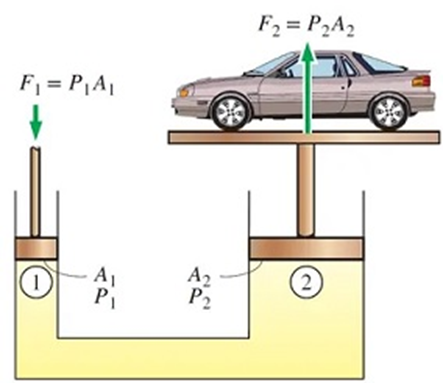
The next example of the application of Pascal’s Law is in hydraulic pumps. Actually, in addition to hydraulic pumps, ordinary bicycle pumps also apply Pascal’s law. The difference is, if you use a hydraulic pump, the power required is much smaller.
-
Hydraulic Brake
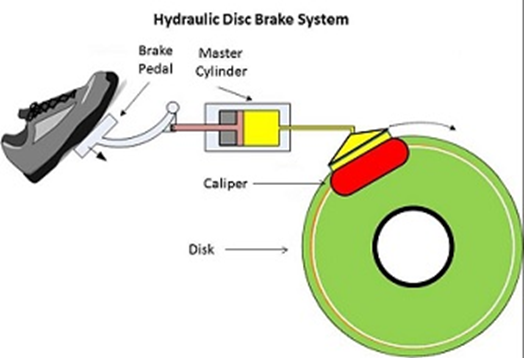
In the automotive industry, especially 4-wheeled vehicles, hydraulic brakes on these wheels work using the principle of paskal law.
When we apply a slight force to the brake pedal with our feet, the master piston will move inside the master cylinder, and the resulting pressure will be transmitted through the brake fluid to work on the piston with a larger surface area.
The advantage of this hydraulic braking system is that the pressure regulated through the pedals is transmitted evenly to all cylinders attached to all four wheels of the car.
-
Cotton Press Machine
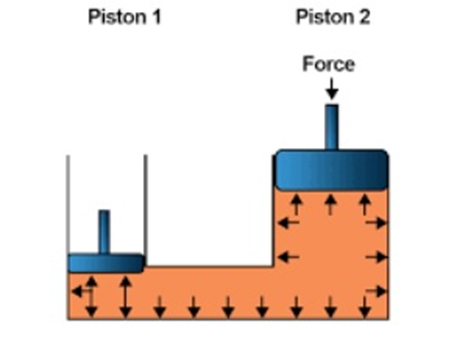
The cotton press also works on the working principle of Pascal’s law. The way it works, when there is a compressive force generated by the machine, the compressive force then presses on the small suction which causes the large suction to move upward to push the cotton until the cotton becomes solid.
-
Aircraft Hydraulic System
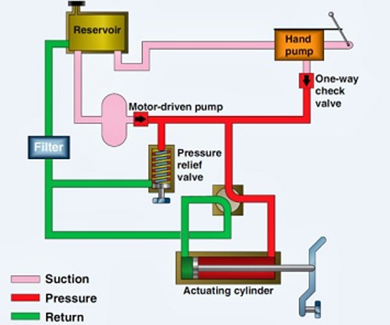
The hydraulic system on an aircraft consists of three mechanical components and hydraulic fluid. Even a small amount of hydraulic fluid helps in transmitting a large amount of pressure force.
Hydraulic fluid in contact with cylinders/pistons is at different pressures. So that oil that is at a relatively higher pressure can be pumped to both sides of the piston head. The selector valve helps in controlling the direction of the liquid. For more details, please see the illustration above.
Also Read: Ohm’s Law
That was a brief explanation of Pascal’s law, starting from the sound of Pascal’s law, working principles, formulas, examples of problems and their application in everyday life. With the explanation from the electronic wiki above, now you understand more about this Paskal law, right?